1，引言：上篇文章“谈谈电力电子器件强迫风冷中风机的工作点”中我谈到曾试图用计算得到函数关系式。但认真地阅读了有关与强迫风冷有关的空气动力学内容后知难而退，感到还不如用试验测得数据较为实际，故文章只介绍了试验方法。事后想想，既然已经了解了一点空气动力学有关计算理论，何不再进一步结合电力电子应用的实际，尝试一下流阻的计算方法。为此参考了一些同行中先行者写的计算流阻的文章，写成此文。目的是希望大家共同来研究、讨论并通过大量的实践来验证和完善这个计算公式。更希望搞通风工程、航空器及空气动力学方面的专家们关注到我们的迫切需要，提出完善的计算方法。所以本文只是一种“抛砖引玉”之举，预计不会有实用价值。需要说明的是平时关注较少，如有电力电子同行知道已有实用文章和计算方法，请积极推荐，在此深表感谢。

　　2，为了便于讨论，全部结构按图二所示进行设定。

　　我们要的是某电力电子设备在初步设计条件下强迫风冷中风量V(m3/小时)和流阻∆P间的函数关系式。然后在风机工作曲线图上(见【图一】)作出流阻曲线，两线交点即为未来的工作点。工作点所对应的风量就是未来工作时的风量。按照【图二】所示的进风口截面积A1换算到风速ω1 (m/s)，查散热器热阻曲线，就可求得散热器长为 时，在该风速下的散热器热阻Rth，根据热阻公式：

　　求得散热器温升。由此可预测所选风机参数是否合适。温升高、易损坏大功率半导体器件，反之，温升过低的设计是不经济的。为了使函数关系式简单明了易于应用，推导中对条件做了若干假定。当然这会带来误差。

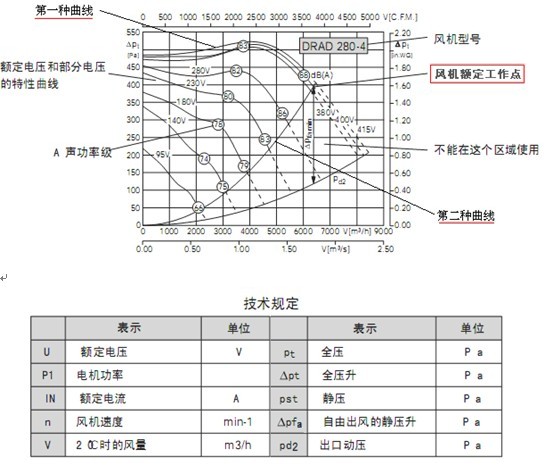
【图一】风机的特性曲线

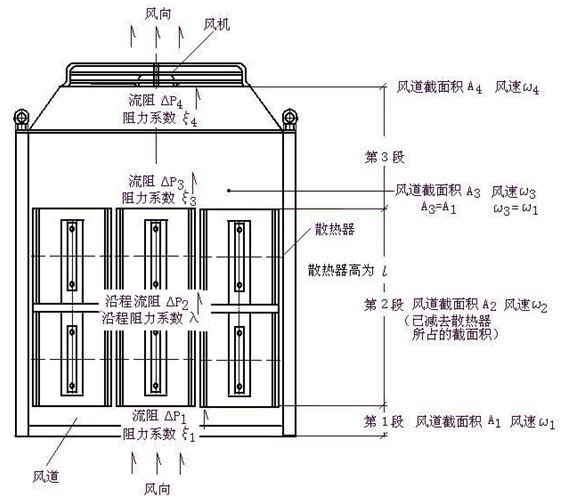
【图二】散热器在风道内强迫风冷状态图

　　3，【图二】把风道分成三段。每段中有关参数图中均已注明，以下内容请对照【图二】阅读。

　　3.1 第一段是进风口，风进入后从散热器底部进入翅片间，通风截面由大突然变小(截面积由A1变成A2)，遇到阻力，即流阻∆P1 ，风速由ω1变成ω2(流阻计算时用风速ω1) 。

　　3.2第二段是散热器所在位置。空气动力学分析此时空气流动产生紊流，造成的阻力 ∆P2

　　称为“沿程流阻”，流阻计算时用风速ω2 。

　　3.3在第三段流动空气从散热器翅片中出来，流动截面由小到大(截面积由A2变成A3，

　　而A3=A1)，此时也会产生流阻 ∆P3 ，流阻计算时用风速ω3 ，由于截面积与第一段一致，

　　故风速ω3=ω1 。

　　3.4第三段上部与风机圈相连。风机圈面积比第三段风道截面积小，通风截面积又由大变小，风速由小变大(由ω3变成ω4)，产生流阻∆P4 。流阻计算时用风速ω4 。

　　这里的∆P1 、∆P3 、∆P4 称为“局部流阻”

　　4，空气动力学给出总流阻及沿程流阻、局部流阻计算公式：

　　总流阻 ∆P = ∆P1 + ∆P2 + ∆P3 + ∆P4

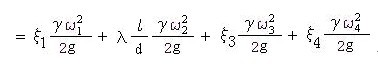
　　式中g 为空气比重，本文中取20℃时的比重：1.128 ， 为 散热器高。

　　其中 x1 x2 x3 为相应段的局部流阻系数，l 为沿程流阻系数。

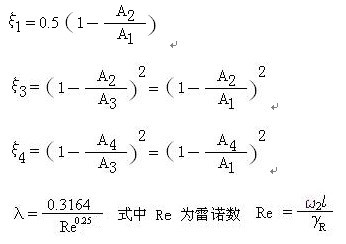
　　2 为第二段的风速，g 为重力加速度，取9.81

　　当量水力直径：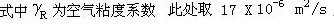

　　5，代入简化后的总流阻：

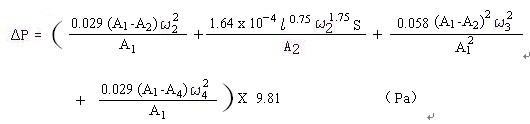
　　化成风量和流阻关系式：

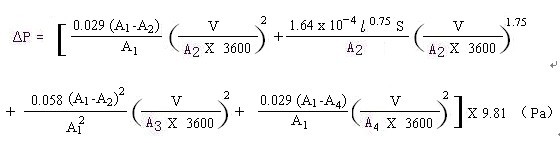
　　根据此式就可作出风量和流阻关系曲线。如能编成计算机计算软件，代入该风道参数A1 、 A2 、 A4 、S、 后即可自动生成 ∆P-V 曲线。

　　(注：本文未完，下次“谈谈电力电子器件强迫风冷中风机的工作点（三）”将举实例进行计算和分析。)

编者简介：朱英文：(1939- )，高级工程师，现任北京京仪椿树整流器有限责任公司技术顾问，中国电力电子产业网特约顾问，主要研究电力半导体器件的设计、制造、应用中的热设计和电力半导体器件主回路结构设计。曾参与专业词典、书籍的编写、翻译等工作。主要成果有：“无刷励磁发电机用旋转整流管设计和制造”，“晶闸管芯片球面磨角工艺”“大功率半导体器件用散热器风冷热阻计算方法”等。