一种新颖的局部阴影条件下MPPT 控制方法

# 技术文库 2012-11-02 08:33 来源：中国电力电子产业网

　　摘要：最大功率点跟踪(maximum power point tracking，MPPT)是光伏发电系统中的重要技术。本文提出一种局部阴影条件下的MPPT 方法，通过切换控制可以实现多极值条件下的MPPT。所做工作通过MATLAB 仿真验证了此方法的有效性，并与已有的两种方法的跟踪性能做了对比。

　　关键词：局部阴影，光伏发电，最大功率点跟踪(MPPT)

　　1.引言

　　随着能源和环境问题的日益突出，太阳能光伏发电以其无污染、储量丰富和分布广泛等优势而备受关注。光伏发电面临着两个主要的问题：(1)光强较低时光伏发电的效率低，(2)I-V 特性曲线受温度、光强的影响呈现出非线性。光伏发电的低效率和高资金投入使得采用MPPT 控制以实时获取最大的能量输出成为光伏发电系统不可缺少的一部分。当温度一定、光强均匀分布时传统的单极值跟踪方法能有效的跟踪到最大功率点(maximum power point，MPP)。然而当存在局部阴影光强分布不均匀时传统的方法可能陷入局部最优点而跟踪不到MPP。尽管目前提出了很多局部阴影条件下的MPPT 控制方法，然而这些算法有自身的不足，比如实现较复杂、全局寻优失效、不能实际应用等。基于此，本文提出一种局部阴影条件下的MPPT控制方法。

　　2.局部阴影条件下光伏阵列的输出特性

　　光伏阵列由光伏模块串并联连接组成。串联连接时，光伏模块一般并联旁路二极管以防止热斑效应，串联后经过防逆流二极管并联。光强均匀分布时P-V特性曲线上只有一个最大功率点。但光强不均匀时，由于旁路二极管和防逆流二极管的存在使得P-V 曲线呈现多极值的特性。

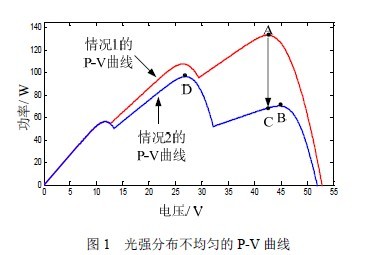
　　光伏阵列的基本单位是光伏电池元[1]，本文的研究工作基于30 个特性一致的电池元串联而成的光伏模块，光伏模块的开路电压Voc=17.85V，短路电流Isc=5.4A，最优工作电压Vopt=13.16V，最优工作电流Iopt=4.87A，最大功率Pmax=64.2W。3 个模块串联连接，图1 给出了两种光强不均匀情况下的P-V 曲线。从图中可以看出P-V 曲线有多个极值点，但只有一个MPP，MPP 的位置随着光强分布的变化而变化。当光强分布为1-0.8-0.6(标幺值1 表示标准光强1000W/m2)，最佳工作点为A 点。当光强分布突变为1-0.7-0.3，工作点从A 点转移至C 点，传统的方法收敛于B 点，但此时D 点才是MPP，因此跟踪不到最大功率点。

　　3.1 新型的控制算法

　　文献[2]给出了一种改进的增量电导法。检测到局部阴影遮挡时MPPT 的参考工作电压Vpv﹡由(1)式给出，式中VocM、IscM 分别为光伏模块的开路电压、短路电流，NsM、NpM 分别为串联、并联模块的数目，Ipv[n]为阴影遮挡时刻的模块电流。采用传统的PI 算法跟踪到Vpv﹡后切换到增量电导法(INC)跟踪MPP。此方法的跟踪性能取决于PI 算法和增量电导法，能否跟踪到MPP 取决于参考电压的准确度。(1)式中只有Ipv[n]是变量，其他参数都固定不变，而Ipv[n]与光强突变前的具体工作点和突变后的光强分布有关，因此这种方法的适应性是有限的

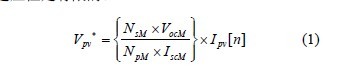
　　文献[3]给出一种基于P-V 曲线扫描的方法。当检测到光强突变时对P-V 曲线扫描，在扫描的过程中找出MPP 所对应的最优占空比信号Dm。扫描结束后直接输出占空比Dm，并采用扰动观察法(P&O)精确跟踪。扫描步长的选择影响此方法的跟踪性能，步长越小，Dm 越接近MPP 所对应的占空比，但扫描时间长损失的能量多。步长越大扫描的时间越短，但得到的Dm 不精确，增加扰动观察法精确跟踪的时间。步长过大将造成Dm 不准，跟踪不到MPP。文献[4]提出功率补偿法。此方法通过给受阴影遮挡的光伏模块补偿一个电压，其大小等于被遮模块与正常模块的工作电压之差，从而使输送到后级变流器的功率在特性曲线上不出现多极值点的特性。功率补偿法能得到各模块最大功率的总和，但此方法需要增加功率补偿单元，硬件投入比较高，另外，增加的补偿电路使得实现起来较复杂。

　　文献[5]提出两步控制法。两步控制法首先通过LC 谐振在线测得光伏电池的短路电流和开路电压。由最佳工作电压、电流与开路电压、短路电流的关系可以得到一条等效负载线。第一步让工作点在等效负载线与I-V 曲线的点处，第一步完成后采用增量电导法精确跟踪MPP。此方法有一个前提：在等效负载线和I-V 曲线的交点右侧只有一个极值点。文献[3]中指出这个前提不是总成立的，当交点右侧存在几个极值点，且MPP 远离交点时，此方法失效。文献[6]提出一种极值比较扰动搜索法，此方法是基于两个重要的结论。

　　(1) MPP 只可能在0.8*Voc(模块的开路电压)的整数倍附近处，因此在搜索的过程中只要扰动步长比0.8 倍的Voc 小就不会遗漏任何极值点,(2)MPP 左侧的极值点呈单调上升趋势，右侧的极值点呈单调递减的趋势，利用这个结论确定极值搜索的方向。然而文献[3]指出这两个前提结论不是总成立的，此时MPPT 可能失败除了上述方法外，还有粒子群优化法,状态空法，Fibonacci 搜索法,神经网络算法，遗传算法，蚁群算法,基于模糊控制的光伏阵列重构等方法。3.2 传统算法与新型拓扑相结合此类解决方案[7]让每个光伏模块都带有MPPT 功能，MPPT 可以采用传统的算法。这种方案能解决由局部阴影引起光伏阵列失配的问题，得到的能量为各光伏模块的最大功率之和。但每个光伏模块都自带MPPT 功能造成系统中变换器、控制器的数量大大增加，因此系统结构复杂、成本较高、可靠性降低。

　　4.伪功率拟合法

　　4.1 伪功率拟合法概述

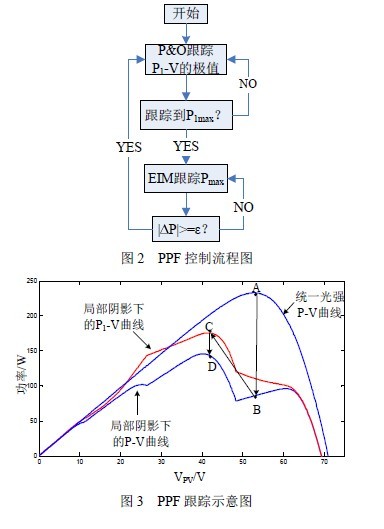
　　本文提出伪功率拟P1-V 呈现出连续、单极值的特性，且极值点P1max 落在真实功率曲线P-V 的最大功率点所在区域。那么用P&O 找到该曲线的极值点P1max 后再切换到P-V 曲线上用等效阻抗匹配法(EIM)精确跟踪MPP。这里将此方法称为伪功率拟合法(pseudo-power fitting，PPF)以区别于其它方法。图2 给出了伪功率拟合法的控制流程图，图3 给出了阴影遮挡情况下的跟踪示意图。光强统一时P-V曲线和伪功率曲线P1-V 重合，首先用P&O跟踪到P1-V曲线的极值点A，跟踪到极值点后切换为EIM 跟踪MPP。当检测到两次采样间隔的功率变化△P 大于阈值ε时认为有局部阴影发生。此时启用P&O 跟踪P1-V曲线的极值点C，将工作点从B 点转移至MPP 所在区域。在极值点C左侧P1-V 曲线的斜率△P1/△V 为正，右侧的斜率为负，因此通过判断△P1/△V 的符号就能确定工作点在极值点C 的左侧还是右侧。当△P1/△V的正负符号变化时认为跟踪到P1-V 曲线的极值点C，此时切换到P-V 曲线上用传统算法EIM 就能跟踪到MPP。

　　4.2 伪功率拟合法的算法构成

　　以串联模块为例，由图1 可知，由于光照不均匀造成模块间不匹配使得P-V 曲线存在多极值。阴影遮挡下的最大功率跟踪复杂的原因正是由于各个模块彼此不能协调工作共同对负载供电。通过分析可知，P-V曲线的每个极值点都对应单个模块的极值点,且极值点右侧与凹陷点区域段电流变化较快。每个凹陷点都是旁路二极管的动作时刻，被旁路二极管短路的模块电压为0(忽略二极管管压降)，输出功率也为0。各模块光强差别(这里不考虑温度)越小，最大功率点处各模块的电压差别也越小。因此可以将这些因素综合起来构成伪功率P1 的组成形式，4 模块串联时伪功率拟合公式采用(2)式。

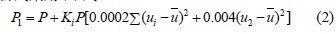
　　公式(2)中ui 表示各模块电压，u2 表示4 个模块电压中数值排第2 的模块电压, ū 表示各模块电压的平均值，Ki=Isc-i，Isc 为标准光强下模块的短路电流，i 为串联支路电流，P 为所有模块的总输出功率。公式中第一项P 是复现功率的总体轮廓。由于光强分布不均匀使得被二极管短路的模块电压、功率都为0，而方差项( i )2 u − u 能反映模块间这种不匹配的情况，此项的极值点出现在二极管由短路到关断时刻，也就是P-V 曲线的凹陷处，故正好能补偿P-V 曲线凹陷区域。2

　　2 (u − u) 与方差项的作用相似，但它的最大值出现在有两个光伏模块短路的凹陷点处，当MPP 处有一、两个模块被二极管短路时，此项能较好的补偿凹陷区域。光强分布一致时22 (u − u) 与方差项都为0，伪功率P1=P。极值点右侧与凹陷点区域段电流下降较快，且功率的变化也快，而系数Ki 是电流的减函数，因此用作修正系数比较合适。功率等级越大需要补偿的量也越大，所以功率P 也被选为修正系数。图3、4 给出了4 个模块串联存在局部阴影情况下的P-V、P1-V 曲线，三种局部阴影的光强分布分别为0.9-0.8-0.7-0.3、1-0.95-0.3-0.2、0.9-0.8-0.6-0.6。图中

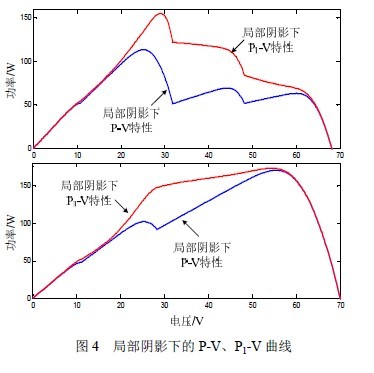
　　P-V 曲线有多个极值点，利用公式(2)得到的P1-V 曲

　　线呈现连续、单极值的特性，且极值点P1max 落在P-V

　　曲线的最大功率点Pmax 所在区域。

　　5.仿真

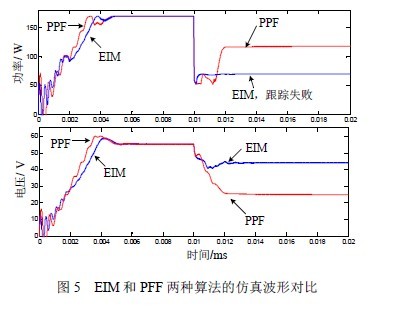
　　通过MATLAB 仿真将伪功率拟合法与传统方法EIM 相比较。光伏电池板由4 个模块串联连接组成，主电路采用Boost 电路，负载为阻性负载。图5 给出了这两种控制方法在局部阴影情况下的功率、电压仿真波形的比较。启动时光强分布为0.9-0.8-0.6-0.6，此时两种控制方法都能跟踪到MPP。10ms 时刻光强分布变化为1-0.95-0.3-0.2，MPP 在小电压区域。此时伪功率拟合法跟踪到了MPP，而EIM 陷入局部最优点跟踪失败。

　　由于EIM 的跟踪性能比INC 优良[8],所以将改进的INC[2]中功率精确跟踪算法用EIM 替代INC 组合成新的算法，定义为改进的EIM。下面将伪功率拟合法

　　(PPF)与扫描法[3]、改进的EIM 做仿真对比，以衡量

　　此方法的跟踪性能。改进的EIM 和PPF 的PI 调节参数选为一致。扫描法的跟踪性能与扫描步长的选择有关，设定占空比的扫描范围为0.2-0.9，经反复比较选择扫描步长为0.002 有较好跟踪性能，精确跟踪的P&O步长选为0.0001图6 给出了3 种控制方法在存在局部阴影情况下的仿真波形比较。启动时光强分布为0.9-0.8-0.6-0.6，MPP 在大电压区域，从图可看出此时3 种控制方法都能跟踪到MPP，扫描法的跟踪时间最长，约为6.5ms，伪功率拟合法的跟踪时间最短,约为5ms, 改进EIM约为5.7ms。10ms 时刻光强分布变化为1-0.95-0.3-0.2,此时伪功率拟合法的跟踪时间最短，约为2 ms，扫描法约为5.3ms，改进的EIM 跟踪时间最长，约为6.5 ms。20ms 时刻光强分布突变为0.9-0.8-0.7-0.3，此时伪功率拟合法和扫描法能跟踪到MPP,跟踪时间分别约为2.8

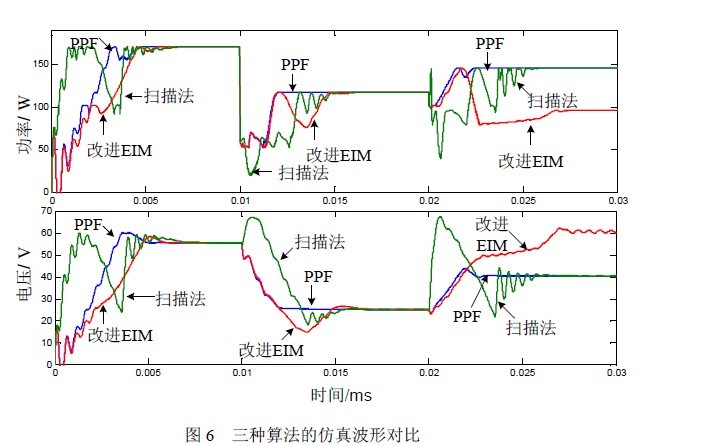
　　ms、5.5 ms，而改进的EIM 跟踪失败。检测到阴影遮挡时扫描法需要一个3.5ms 的固定扫描时间，且扫描期间功率、电压变化范围大，扫描结束后的跟踪过程中功率、电压有较大的波动，这是由于扫描结束后从输出占空比Dm 到电路稳定运行需要一个动态调节过程。从算法本身来看，改进的EIM在启动时没有抑制局部阴影的作用(存在局部阴影时可能跟踪不到MPP)，检测到有阴影遮挡时此算法依靠公式(1)得到参考电压来判断MPP 的所在区域，参考电压不但受光强突变后光强的影响，而且还与光强突变前工作点的具体位置有关。20ms 时刻由公式(1)得到的参考电压约为54V，不在MPP 所在区域，因此MPPT 失败，10ms 时刻光强分布突变，改进的EIM 由公式得到参考电压约为14V，而MPP 的电压约为24.5V,因此跟踪时间比其它两种方法长。而伪功率拟合法直接跟踪伪功率P1-V 曲线的极值点，且此极值　接近于MPP，因此具有较快的跟踪速度。虽然伪功率拟合公式在一定的光强分布下能拟合出连续、单极值的P1-V 曲线，与改进的EIM 类似，它的适应范围也是有限的。4 模块串联的拟合算式(2)适应大部分光强不均匀的情况，但串联模块数量增多时拟合公式需要做进一步研究，同时此方法需要检测各模块的电压，增加了采样电路的复杂性。相比之下只要扫描步长选择足够小，负载阻抗的选择满足阻抗匹配的要求，扫描法总能跟踪到各种光强分布下的

　　MPP。

　　6.结论

　　局部阴影遮挡时，光伏阵列的P-V 曲线上有多个极值点，传统单极值的MPPT 方法可能陷入局部最优点而跟踪不到MPP。本文从P-V 曲线多极值形成原因的角度提出了一种局部阴影遮挡下的MPPT 控制方法--伪功率拟合法,通过MATLAB 仿真软件验证了此方法的有效性。并与扫描法、改进的EIM 相比较证明　适应的光强范围内此方法具有良好的跟踪性能。

　　参考文献

　　[1] 刘邦银,段善旭,康勇.局部阴影条件下光伏模组特性的

　　建模与分析[J].太阳能学报,2008,29(2):188-192

　　[2] Young-Hyok Ji, Doo-Yong Jung. “Maximum Power Point

　　Tracking Method for PV Array under Partially Shaded

　　Condition” Energy Conversion Congress and Exposition,

　　2009. ECCE 2009.IEEE.pp307-312

　　[3] Kazmi, S.; Goto, H.; Ichinokura, O.; Hai-Jiao Guo; , "An

　　improved and very efficient MPPT controller for PV

　　systems subjected to rapidly varying atmospheric

　　conditions and partial shading," Power Engineering

　　Conference, 2009. AUPEC 2009. Australasian