摘 要:在三相并网逆变器中采用 LCL 型滤波器可以有效地滤除输出电流的高次谐波,并且在低频时,较单电感达到相同的滤波效果,其取值更小。由于LCL 滤波器是3 阶非线性系统,容易使逆变系统稳定性变差,本文采用了直流侧电压外环,基于dq 坐标系下的逆变器侧电流内环的控制策略避免了网侧电流反馈时比例增益受限制的影响,为了进一步提高并网功率因数,加入了LCL 滤波电容电流前馈补偿的控制策略,同时去除LCL 中滤波电容电阻,引入虚拟阻尼的方法,增强了系统的稳定性,通过仿真验证了该方法的可靠性。
1.引言
随着能源短缺问题的不断加剧,新能源的开发与利用受到越来越广泛的研究,由此衍生的逆变技术也逐渐受到国内外学者的重视。由于逆变器输出电流的高次谐波较多,在此采用了LCL 型系统,其在高频时相当于一个三阶的滤波器,可以使高次谐波受到明显抑制,尤其是对开关频率处的谐波抑制效果更佳明显。
文献[1]对采用LC 型滤波器的控制方法进行了研究,虽然其工作在独立带负载时能起到很好的高次谐波滤除效果,但是工作在并网模式时,其滤波电容近似于负载,不能起到滤波的作用。采用LCL 滤波器会对系统产生较大的谐振影响,文献[2]和[3]采用了滤波电容中串电阻的方法来抑制滤波器的谐振,但是串入的电阻会产生额外的功率损耗。文献[4]采用了LCL 滤波器的网测电流反馈控制,由根轨迹分析其系统的比例增益的取值范围有限,若超出取值范围可能使系统不稳定。本文采用了基于dq 坐标系下的逆变器侧电流内环的控制策略避免了网侧电流反馈时比例增益受限制的影响,为了进一步提高并网功率因数,加入了LCL滤波电容电流前馈补偿的控制策略,同时去除LCL 中滤波电容电阻,引入虚拟阻尼的方法,增强了系统的稳定性。通过MATLAB/SIMULINK 仿真验证了该方法的可靠性,并考虑到电网电压幅值的瞬间跌落对系统的影响,应用此方法可以有效的维持其稳定性。
2.LCL 型并网逆变器数学模型
图 1 中,ea,eb,ec 是三相电网的相电压;igk(k=a,b,c)为LCL 型滤波器的网侧相电流;iik(k=a,b,c)为LCL 型滤波器的变换器侧的三相输出相电流;ica,icb,icc 为LCL 型滤波器中的滤波电容电流,uca,ucb,ucc 为LCL
滤波器中的电容的电压;Lg为LCL滤波器的网侧电感,其中Rg 为电感的寄生电阻;Li 为LCL 滤波器的变换器侧电感,其中Ri 为电感寄生电阻;Cf 为LCL 滤波器的滤波电容,其中Rf 为阻尼电阻,能有效的避免出现零阻抗谐振点;VT1~6 为变换器的开关器件;Cdc 为直流侧电容;udc 为直流侧输入电压;iin 为直流电源输入电流;idc 为变换器的支流输入电流。

由于 LCL 型滤波器与L 型滤波器在低频段的特性是相同的,且LCL滤波器主要起滤除高频谐波的作用,为方便控制器的设计,在此忽略滤波器中的阻尼电阻及滤波电容的影响,得到其在dq 坐标系下的数学模型为

2.1 LCL 型滤波器的参数选择
初步确定所设计逆变器的参数如表1

设逆变器输出的相电流有效值为I,逆变器输出的
相电流峰值Im,则
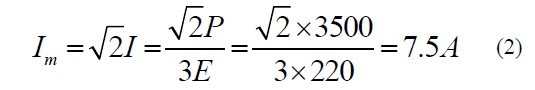
为得到更好的滤波效果,本文从总电感量、谐振频率限制、纹波抑制和无功功率要求等方面进行LCL滤波器参数的选择
2.1.1 总电感量L 的选取条件

由图 2 可知,在转折频率以下时,LCL 滤波器相当于单电感L 滤波器,二者有一样的滤波效果。要实现变换器的双向功率传输[2],需满足下式
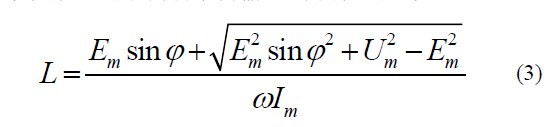
式中: 为电网电压角频率,Em 为电网相电压峰值,Im 为相电流峰值,Um 为变换器侧输出相电压基波峰值。在本文控制方法中,采用SVPWM 调制算法,故可得Um=Udc/3,则

代入数据可得L≤0.089184。等效单电感时,不仅要考虑滤波电感的功率损耗及控制时的快速电流跟踪,还需要抑制变换器在开关频率处的谐波,参考电流脉动允许值的要求[2],按式
(5)进行设计
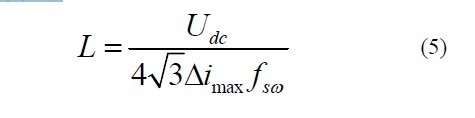
式中, imax 为谐波电流的最大纹波电流,通常取值为额定电流的10%~20%,在这里取20%,带入相关数据可得L≥0.006255。从功率损耗和电流跟踪快速性来考虑,总电感量L 应越小越好;但是从滤波效果来看,L 应越大越好。因此,在总电感量的选择上应综合考虑两方面的影响。
2.1.2 电感Lg 和Li 的选择
为了减小对系统的谐振影响,LCL 滤波器的谐振频率fres 满足如下关系式[5]
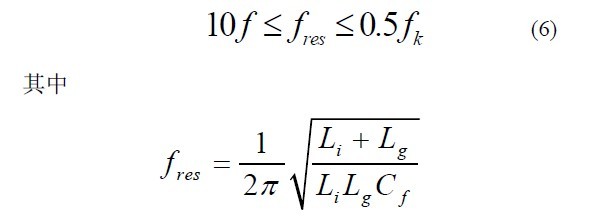

网侧电感[7]一般取Lg=K*Li, K=0~1。取K=0.2,0.5,1,如图所3 示,K 值越大,LCL 滤波器的衰减特性越大,但在转折频率之前的衰减特性一样,由于电感越大,滤波器的体积也越大,考虑到损耗的问题,通常情况下取K=0.5,则Lg=7.05mH。
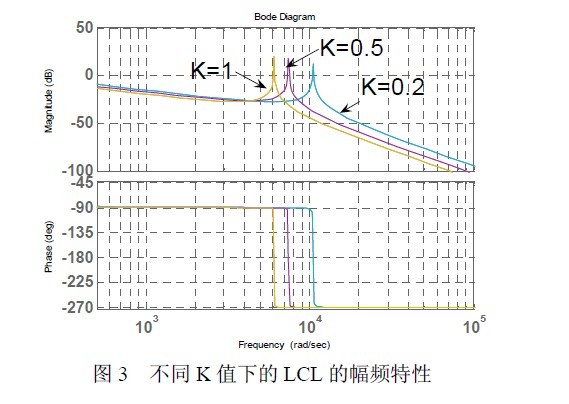
2.1.3 滤波电容Cf 的选取
由于 LCL 滤波器中加入了滤波电容会增加系统的无功功率的损耗,为了使系统在较高功率因数下运行,通常会限制无功功率小于系统额定有功功率的5%。由文献[5]可得滤波电容的限制条件
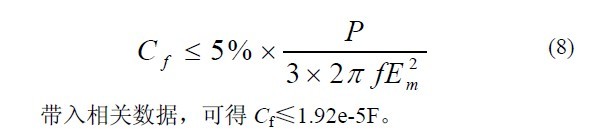
由于不能使电感值太大,所以电容值不能选的太小。因此,在设计电容参数时,初始值可以选为最大值的一半左右,然后经过仿真多次调整得到最佳值。
2.2 多环控制侧略
逆变器侧电流反馈的系统根轨迹极点基本上全部分布于复平面的左半部分,使得比例增益有较大的调节范围,稳定性增强,如图4。
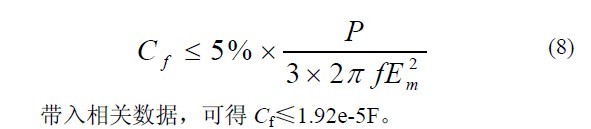
如图 5 所示,将电容支路电流前馈于网侧电流指令信号上,其和作为逆变器侧电流反馈的参考信号,从而通过逆变器侧电流反馈间接控制并网电流。电容支路电流前馈的增加保证逆变器以较高功率因数向电网回馈电能。
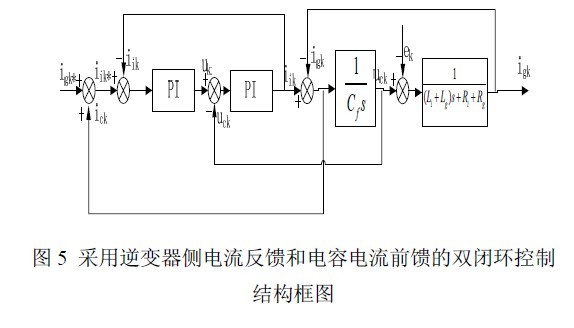
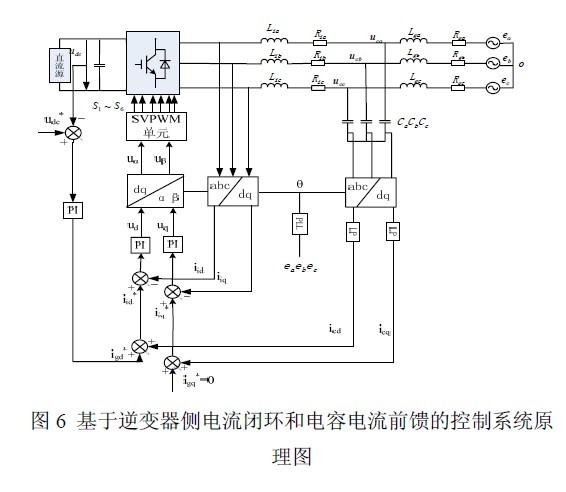
图 6 基于逆变器侧电流闭环和电容电流前馈的控制系统原理图
控制系统的原理结构图如图6 所示。同步旋转坐标系下,直流电压外环的输出作为并网电流的给定,并由电网电压矢量定向;为保证系统单位功率因数运行,并网电流q 轴分量设定为零。通过低通滤波器处理的电容支路电流与并网电流指令信号的dq 轴分量相加作为逆变器侧电流内环给定,然后经过帕克反变换得到两相静止坐标系下有源逆变器输出电压的调制信号和,将它们送入空间矢量脉宽调制(spacevector pules width modulation,SVPWM)单元生成三相桥路的PWM 驱动信号。
2.3 虚拟阻尼法
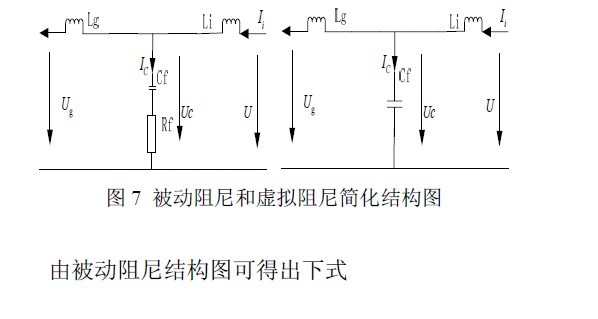
为了消除系统的高次谐波,并且考虑到功率损耗,转换效率等,采用虚拟阻尼法代替被动阻尼法。虚拟电阻的方法是通过反馈电容电压或电流,构成多变量反馈系统,避免谐振产生,其效果等同于在滤波电路中串入一个真实的电阻[8]。简化 LCL 电路图,忽略网侧电感的寄生电阻和变换器电感的寄生电阻,则被动阻尼和虚拟阻尼技术如图7。
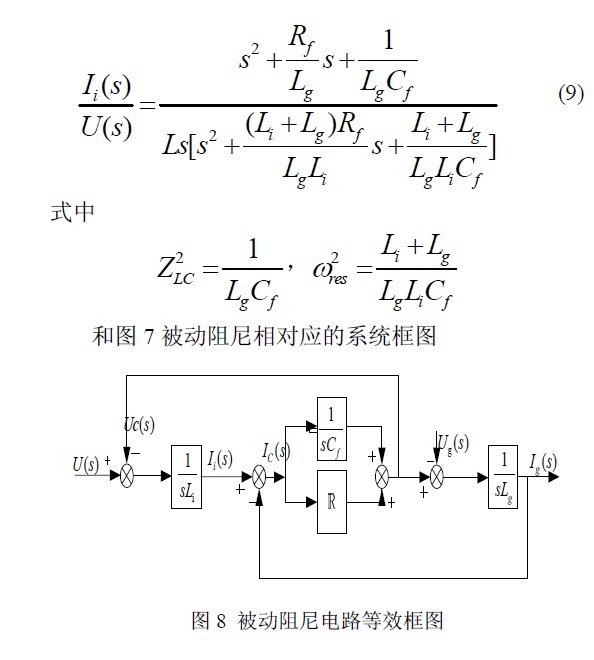
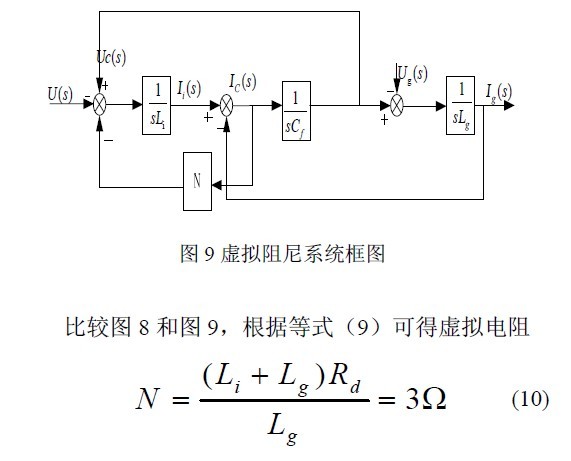
在图 8 中的电阻可以通过框图变换,在不影响系
统输出的情况下引出虚拟电阻,如图9 中的阻尼电阻M
3.仿真分析
根据 2.1 节的设计参数,在MATLAB/SIMULINK下搭建系统模型进行仿真验证,其中PI 调节器参数:电压环节Kvp=0.5,Kvi=60;电流环节Kip=20,Kii=120。由所采取的控制方法得入网电流与电网电压的关系如下图所示
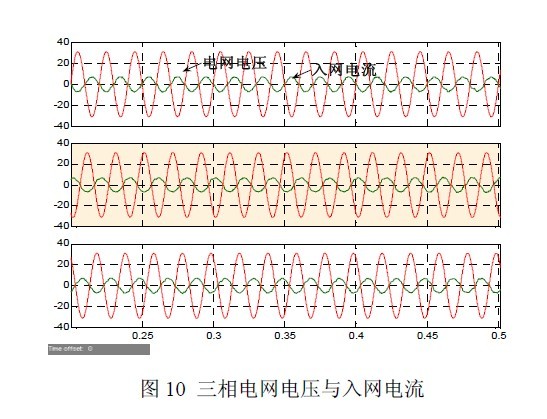
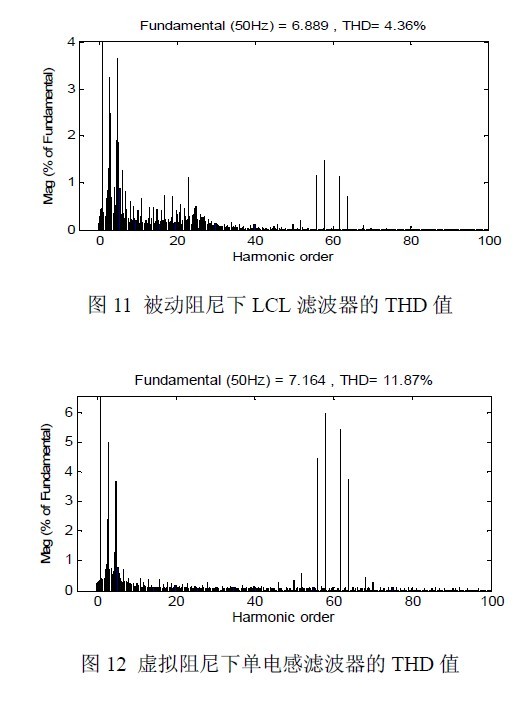
图 10 所示电网电压和入网电流,将电网电压值缩小10 倍,入网电流的有效值为4.95A,功率因数可以达到-0.98。图 11 为被动阻尼下LCL 滤波器的入网电流的THD 值,图12 和图13 分别为L 型和LCL 型滤波器时的入网电流在虚拟阻尼下的THD 值,可知LCL 型滤波器有很好的滤波效果,并且能够很好的抑制高次谐波,尤其是对开关频率处3KHz 处的谐波抑制,有效地减小了入网电流的谐波畸变率。由图11 和图13可知虚拟阻尼可以达到与被动阻尼同样的效果。
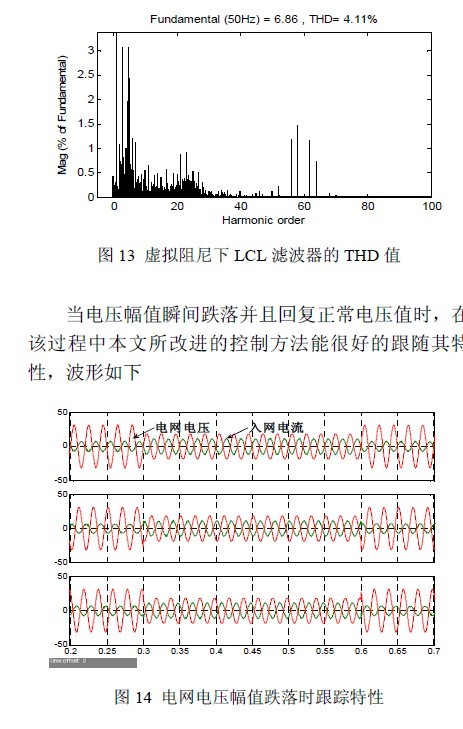
其并网功率因数并未因电网电压幅值跌落而受到较大影响,仍维持在-0.98。由图15 可知在电网电压跌落期间,该方法仍可有效减小入网电流的THD 值。结合图13 可知当入网电流较大时,其入网电流的谐波抑制效果越好。


4.结论
通过LCL 滤波器可以有效的抑制入网电流的高次谐波,尤其是对开关频率处的抑制效果更加明显,入网电流的基波畸变率得到了明显的减小。采用逆变器侧电流反馈控制和滤波电容电流前馈控制可以显著增强系统稳定性,使并网功率因数维持在近似单位因数。引入虚拟阻尼法,可以有效地减少功率损耗,其效果与有阻尼效果一样。在电网电压幅值瞬间跌落时能够有效的跟踪其变化,使并网功率因数维持恒定。
参考文献
[1] 梁超辉,刘邦银,段善旭。基于滤波电容电流补偿的并网逆变器控制[J]. 电力电子技术,2008,42(8): 13-15.
[2] Wang T C,Ye Z H,Sinha G, etal. Output filter design for agrid-interconnected three-phase inverter[c]. USA:PowerElectronics Specialist Conference,2003:779-984.
[3] ROUTIMO M, TUUSA H. LCL type supply filter foractive power filter-comparison of an active and a passivemethod for resonance damping[C]. The 38th IEEE PowerElectronics Specialists Conference. O rlando, Florida,USA: IEEE, 2007: 2939 2 2945.
[4] 王要强,吴凤江,孙力. 并网逆变器LCL 滤波器新型有源阻尼控制[J]. 电力自动化设备,2011,31(5):75-79.
[5] Liserre M, Blaabjerg F, Hansen S. Design and control ofan LCL-filter based three-phase active rectifier[j]. IEEETransactions on Industrial Applications, 2005, 41(5):1281-1291.
[6] Bernet S, Ponnaluri S, Teichmann R. Design and losscomparison of matrix converters and voltage sourceconverters for modem ac- drives[J]. Transaetion ofIndustrial Eleetronics Soeiety,2002,24(6):146-150.
[7] 汪飞. 可再生能源并网逆变器的研究[D]. 杭州:浙江大学,2005.
[8] 葛昂. 带有LCL 滤波器的变频器能量回馈控制策略研